耿雨飞的个人博客

[[ slide_text ]]

[[ item.c ]]

面试题算法题

发布时间：2023-03-23 作者：gengyufei 来源：gengyufei个人博客

数据结构与算法 面试集锦

# 简单
## 消失的数字
### 题目描述
数组nums包含从0到n的所有整数，但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗？
注意：本题相对书上原题稍作改动
```
示例 1：
输入：[3,0,1]
输出：2

示例 2：
输入：[9,6,4,2,3,5,7,0,1]
输出：8
```
### 题解
```
class Solution(object):
    def missingNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        return sum(range(len(nums)+1)) - sum(nums)
```
## 反转链表
### 题目
给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。
示例 1：
![](https://assets.leetcode.com/uploads/2021/02/19/rev1ex1.jpg)
```
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]
```

示例 2：
![](https://assets.leetcode.com/uploads/2021/02/19/rev1ex2.jpg)
```
输入：head = [1,2]
输出：[2,1]
```

示例 3：
```
输入：head = []
输出：[]
```

> 提示：
链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

### 题解
解题思路：
要将链表 ```1 -> 2 -> 3 -> 4 -> Null``` 反转为 ```4 -> 3 -> 2 -> 1 -> Null``` ，需要一个 cur 指针表示当前遍历到的节点；一个 pre 指针表示当前节点的前驱节点；在循环中还需要一个中间变量 temp 来保存当前节点的后驱节点。

算法流程：
- 首先 pre 指针指向 Null，cur 指针指向 head；

- 当 cur != Null，执行循环。

- 先将 cur.next 保存在 temp 中防止链表丢失：temp = cur.next

- 接着把 cur.next 指向前驱节点 pre：cur.next = pre

- 然后将 pre 往后移一位也就是移到当前 cur 的位置：pre = cur

- 最后把 cur 也往后移一位也就是 temp 的位置：cur = temp

- 当 cur == Null，结束循环，返回 pre。

**图解流程**：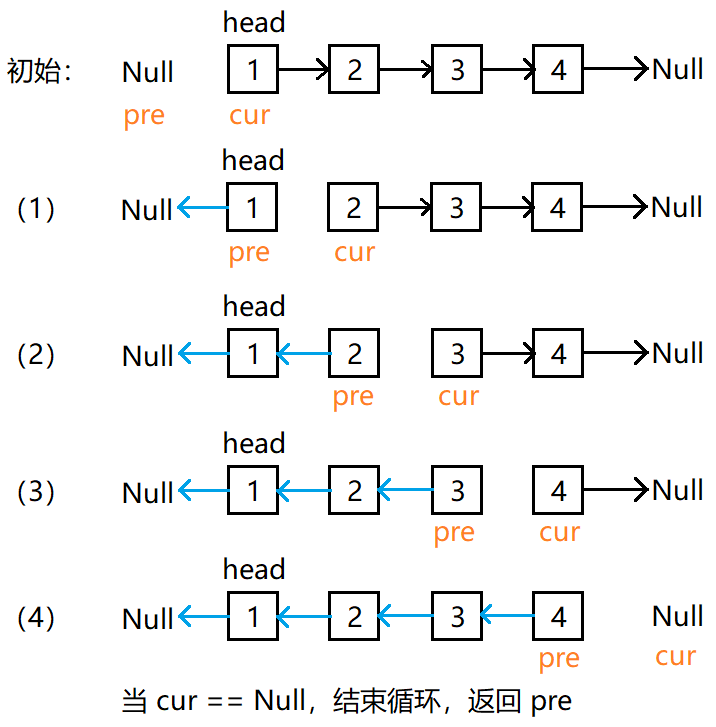
![](https://pic.leetcode-cn.com/039a6eff23111dba77d91ed909bbd35539b1185c07664372b129216a7b779b4a-image-20200627220535158.png)

代码：
```
# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        pre = None
        cur = head
        while cur:
            temp = cur.next   # 先把原来cur.next位置存起来
            cur.next = pre
            pre = cur
            cur = temp
        return pre
```

## 有效的括号
### 题目描述
给定一个只包括``` '('，')'，'{'，'}'，'['，']' ```的字符串 s ，判断字符串是否有效。

有效字符串需满足：

- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。

示例 1：
```
输入：s = "()"
输出：true
```
示例 2：
```
输入：s = "()[]{}"
输出：true
```
示例 3：
```
输入：s = "(]"
输出：false
```

> 提示：
1 <= s.length <= 104
s 仅由括号 '()[]{}' 组成

### 题解
当开始接触题目时，我们会不禁想到如果计算出左括号的数量，和右括号的数量，如果每种括号左右数量相同，会不会就是有效的括号了呢？

事实上不是的，假如输入是 ```[{]}```，每种括号的左右数量分别相等，但不是有效的括号。这是因为结果还与括号的位置有关。

仔细分析我们发现，对于有效的括号，它的部分子表达式仍然是有效的括号，比如 ```{()[()]}``` 是一个有效的括号，```()[{}]```是有效的括号，```[()]``` 也是有效的括号。并且当我们每次删除一个最小的括号对时，我们会逐渐将括号删除完。比如下面的例子。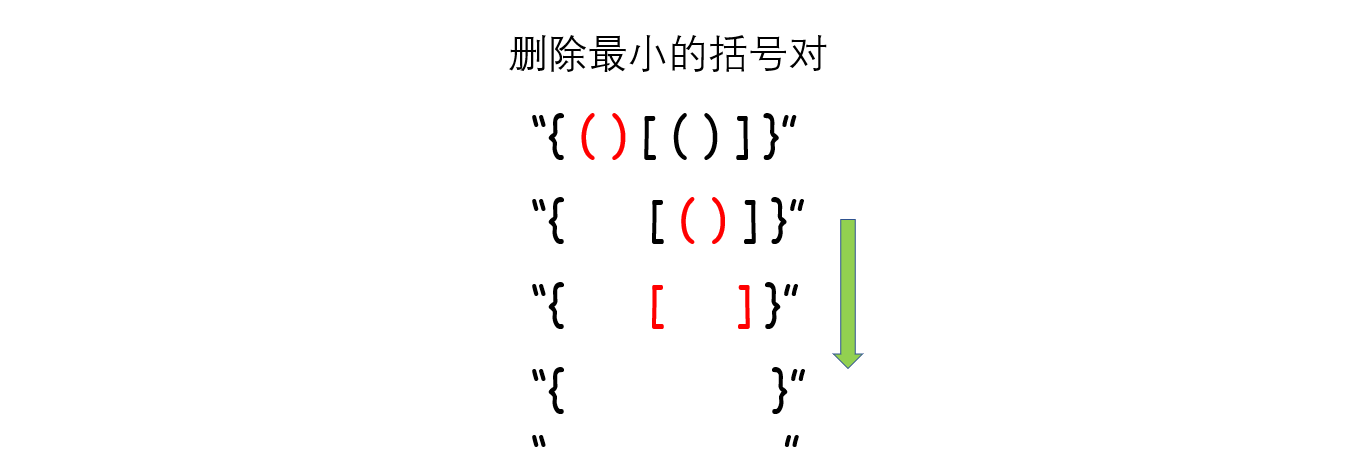

![](https://pic.leetcode-cn.com/467248403853f33e0dabd80c644893ad22aa6069f261bd6a4c4d62e3d7df2f8c-p1.png)

这个思考的过程其实就是栈的实现过程。因此我们考虑使用栈，当遇到匹配的最小括号对时，我们将这对括号从栈中删除（即出栈），如果最后栈为空，那么它是有效的括号，反之不是。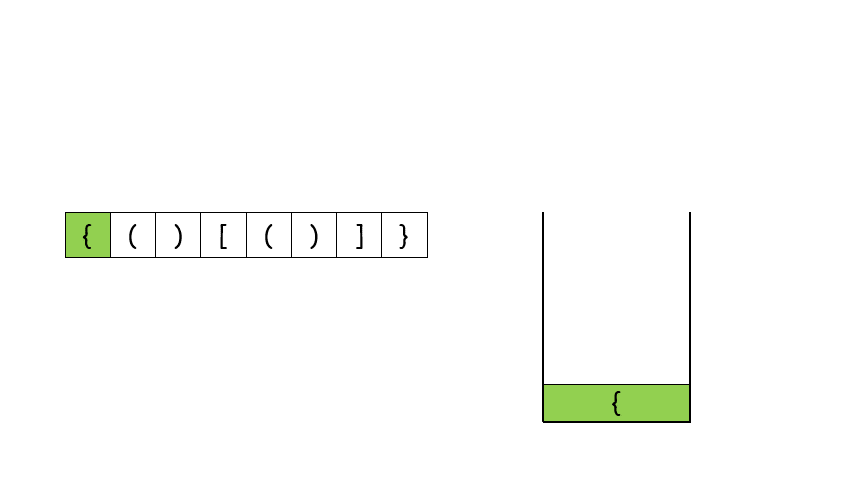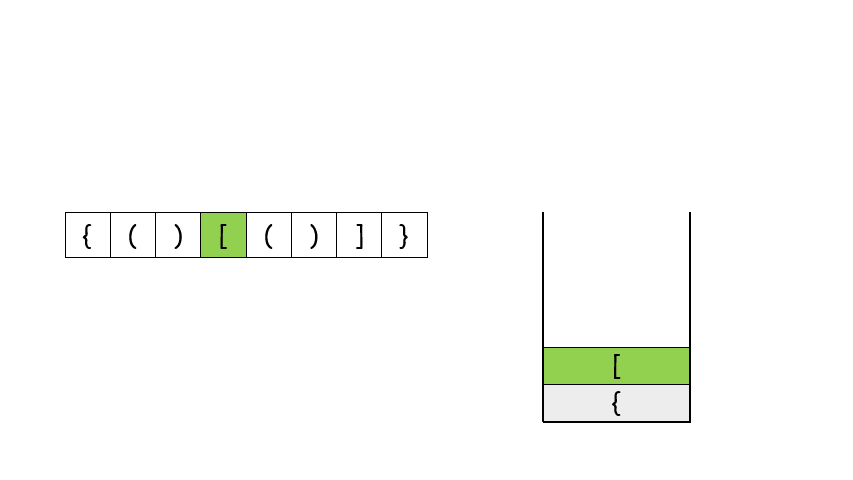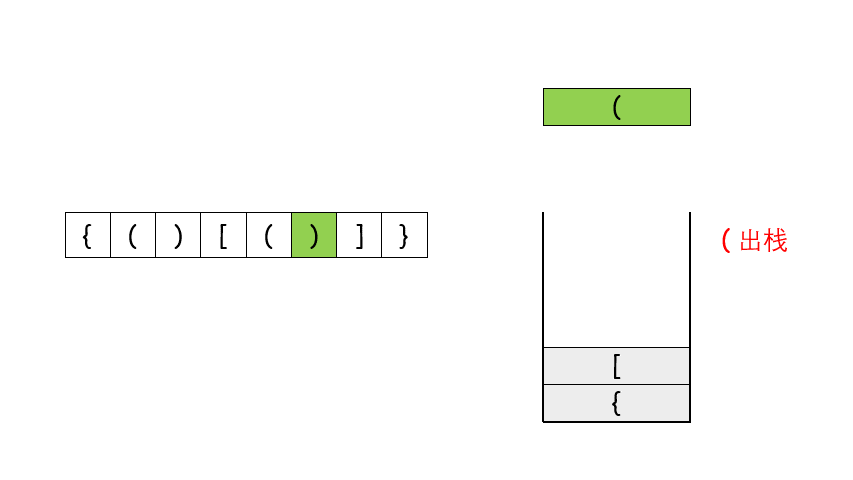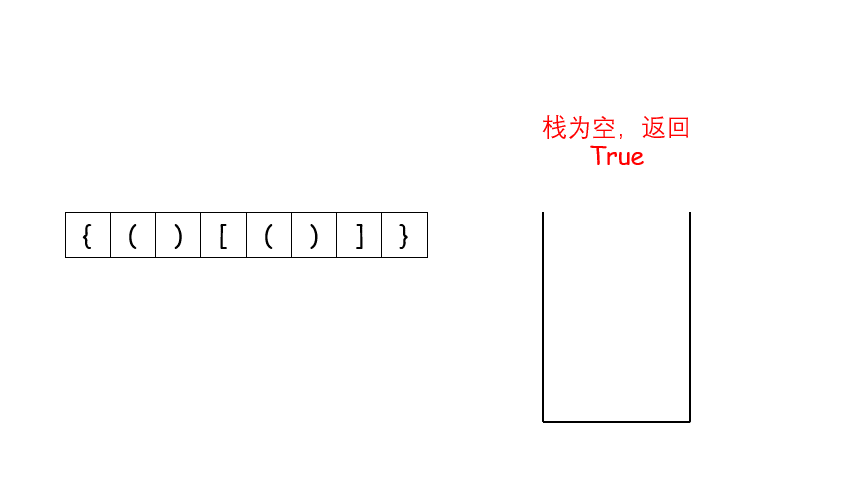

![](https://pic.leetcode-cn.com/baa8829ac398e665eb645dca29eadd631e2b337e05022aa5a678e091471a4913-20.gif)

代码
```
class Solution:
    def isValid(self, s: str) -> bool:
        dic = {')':'(',']':'[','}':'{'}
        stack = []
        for i in s:
            if stack and i in dic:
                if stack[-1] == dic[i]:
					stack.pop()
                else:
					return False
            else: stack.append(i)
        return not stack
```

## 两数之和
### 题目描述
给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。
示例 1：
```
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
```

示例 2：
```
输入：nums = [3,2,4], target = 6
输出：[1,2]
```
示例 3：
```
输入：nums = [3,3], target = 6
输出：[0,1]
```

> 提示：
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案

进阶：你可以想出一个时间复杂度小于 O(n2) 的算法吗？

### 题解
```
class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        hastable=dict()
        for i, num in enumerate(nums):
            if target-num in hastable:
                return [i,hastable[target-num]]
            hastable[num]=i
        return []
```

# 中等
## 无重复字符的最长字串
### 题目补充
给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
```
输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。
```

示例 2:
```
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。
```

示例 3:
```
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。
```

提示：
> 0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成

### 题解
#### 滑动窗口
**思路和算法**

我们先用一个例子考虑如何在较优的时间复杂度内通过本题。

我们不妨以示例一中的字符串 abcabcbb 为例，找出从每一个字符开始的，不包含重复字符的最长子串，那么其中最长的那个字符串即为答案。对于示例一中的字符串，我们列举出这些结果，其中括号中表示选中的字符以及最长的字符串：

- 以 (a)bcabcbb 开始的最长字符串为 (abc)abcbb；
- 以 a(b)cabcbb 开始的最长字符串为 a(bca)bcbb；
- 以 ab(c)abcbb 开始的最长字符串为 ab(cab)cbb；
- 以 abc(a)bcbb 开始的最长字符串为 abc(abc)bb；
- 以 abca(b)cbb 开始的最长字符串为 abca(bc)bb；
- 以 abcab(c)bb 开始的最长字符串为 abcab(cb)b；
- 以 abcabc(b)b 开始的最长字符串为 abcabc(b)b；
- 以 abcabcb(b) 开始的最长字符串为 abcabcb(b)。

发现了什么？如果我们依次递增地枚举子串的起始位置，那么子串的结束位置也是递增的！这里的原因在于，假设我们选择字符串中的第 k 个字符作为起始位置，并且得到了不包含重复字符的最长子串的结束位置为 rk。那么当我们选择第 k+1 个字符作为起始位置时，首先从 k+1 到 rk 的字符显然是不重复的，并且由于少了原本的第 k 个字符，我们可以尝试继续增大 rk，直到右侧出现了重复字符为止。

这样一来，我们就可以使用「滑动窗口」来解决这个问题了：

- 我们使用两个指针表示字符串中的某个子串（或窗口）的左右边界，其中左指针代表着上文中「枚举子串的起始位置」，而右指针即为上文中的 rk

- 在每一步的操作中，我们会将左指针向右移动一格，表示 我们开始枚举下一个字符作为起始位置，然后我们可以不断地向右移动右指针，但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后，这个子串就对应着 以左指针开始的，不包含重复字符的最长子串。我们记录下这个子串的长度；

- 在枚举结束后，我们找到的最长的子串的长度即为答案。

**判断重复字符**

在上面的流程中，我们还需要使用一种数据结构来判断 是否有重复的字符，常用的数据结构为哈希集合（即 C++ 中的 std::unordered_set，Java 中的 HashSet，Python 中的 set, JavaScript 中的 Set）。在左指针向右移动的时候，我们从哈希集合中移除一个字符，在右指针向右移动的时候，我们往哈希集合中添加一个字符。

至此，我们就完美解决了本题。
```
class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        # 哈希集合，记录每个字符是否出现过
        occ = set()
        n = len(s)
        # 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
        rk, ans = -1, 0
        for i in range(n):
            if i != 0:
                # 左指针向右移动一格，移除一个字符
                occ.remove(s[i - 1])
            while rk + 1 < n and s[rk + 1] not in occ:
                # 不断地移动右指针
                occ.add(s[rk + 1])
                rk += 1
            # 第 i 到 rk 个字符是一个极长的无重复字符子串
            ans = max(ans, rk - i + 1)
        return ans
```
**复杂度分析**
- 时间复杂度：O(N)，其中 N 是字符串的长度。左指针和右指针分别会遍历整个字符串一次。

- 空间复杂度：O(∣Σ∣)，其中 Σ 表示字符集（即字符串中可以出现的字符），∣Σ∣ 表示字符集的大小。在本题中没有明确说明字符集，因此可以默认为所有 ASCII 码在 [0, 128) 内的字符，即 ∣Σ∣=128。我们需要用到哈希集合来存储出现过的字符，而字符最多有 ∣Σ∣ 个，因此空间复杂度为O(∣Σ∣)。

# 困难

上一篇：面试题通用基础面试题下一篇：面试题数据库

你觉得文章怎么样

耿雨飞的个人博客

面试题 算法题

面试题算法题